Statistical framework
Progress (December 2019)
Following a short pause, and with the additional of Aoibheann Brady and Yann Ziegler to our team, we have resumed development of the BHM framework to explore vertical land motion (VLM) for North America, with the aim of separating the signal into its GIA and mass change components.
The main innovation in our latest work has been a switch to a ‘time-evolving’ solution. Previously, all our deployments of the BHM at a global scale have involved a ‘time-invariant’ approach; that is trends for a given time period represented by a single average value. The time-evolving solution – which we had always intended to move towards as the project progressed – instead considers a time-series of data points. While this means that both data and computational requirements are greater, it should help us separate different sources and will provide us with time-evolving output which should tell us more about the underlying processes that contribute to sea level rise.
We hope to have our first time-evolving output for North America early in 2020.
Progress (May 2018)
We have continued to work on what is the first real test of the Bayesian Hierarchical Model (BHM) framework on a global scale – using the framework to ‘predict’ global steric sea level change.
It has become clear that the way in which we use observations as ‘inputs’ – and specifically the way in which we define errors associated with the observations – becomes critical to the ability of the BHM to produce physically-realistic outputs. Nowhere is this more important than for the GRACE data which, via measured changes in gravity anomalies, allows us to infer changes in water and ice mass through time.
The GRACE data tends to be heavily processed and is available in multiple formats, so we have spent time ensuring that we (i) are using the most appropriate GRACE data, (ii) understand exactly what processing has been done and (iii) have correctly specified the errors.
In parallel to this, we have also been developing the BHM itself so that it is better able deal with the eccentricities of the GRACE data, by exploring different ways in which we can treat the mass process. For example, whether it is assumed to be ‘stationery’ and treated in the same way everywhere or whether it is assumed to be ‘non-stationery’ and treated in different ways over land and ocean.
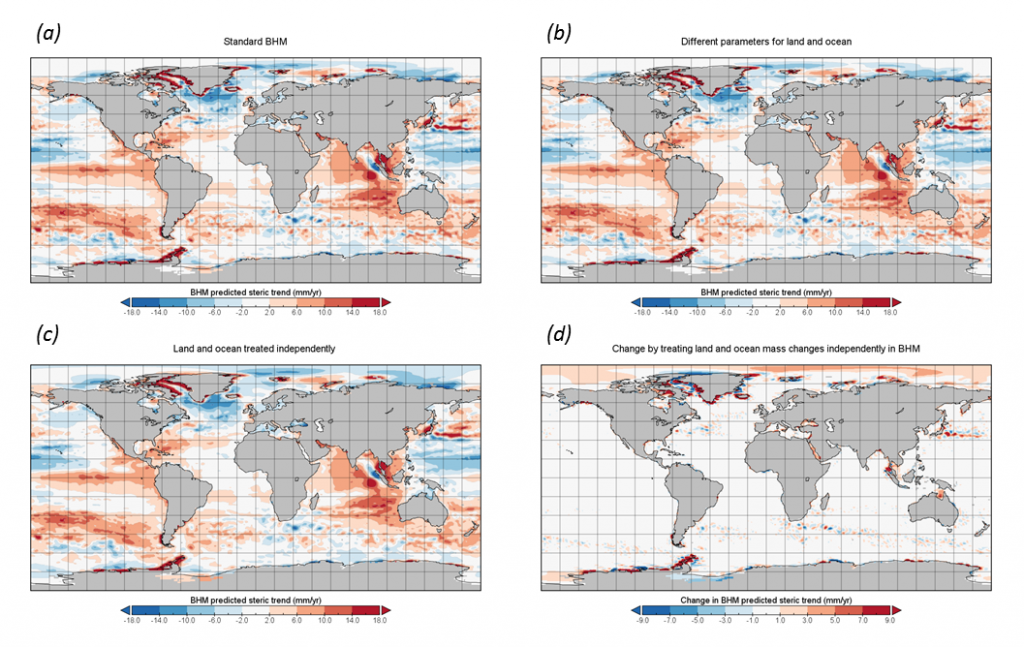
Figure 1. An example of how treating the GRACE data in different, yet plausible, ways produces different spatial patterns of predicted steric sea level change. Plot (a) treats the data in the same way everywhere, while (b) and (c) show two contrasting ways of treating land and oceans differently. Plot (d) shows the difference these assumptions can make on the final BHM-predicted sea level trend.
Progress (April 2018)
A major focus of the project over its first 18 months has been the development and testing of the Bayesian Hierarchical Model (BHM) – the statistical framework that is fundamental to the GlobalMass project. It is essential that the framework is working correctly before we can start to add in more data and use it to derive geophysical results.
We have extended the BHM framework from resolving regional processes on a cartesian grid (as used previously, for example in the NERC-funded RATES project) to global processes operating on a sphere, and have proposed two generic models for dealing with non-stationarity of the global process. As such, the framework now has a potentially wide range of global data assimilation applications.
In addition, we have developed and tested a more efficient approach for solving the stochastic partial differential equations in the BHM known as INLA (Integrated Nested Laplace Approximation). This is an important step, as it is computationally more efficient, which was a technical constraint for the implementing the BHM at a global scale with adequate resolution.
Next page: Outputs
